|
教訓:音楽家は数学の先生から逃げ出した、とAdornoが言った。 多分そうだろう、それなら音楽の先生からも逃げたほうがいい、と私なら言う。 Vorbemerkung (序文) 数学のテーマの中にて人間が最も分かれるところは複素数(コンプレックスナンバー)についてである。 人 間は2つの人種に分かれているように思う:理解出来ている人、そして理解出来ない人(理解したくない 人)だ。 繊細な音楽家にこのような難しい(笑)トピックスについてあまり提示させたくない(教訓として 言うように) しかしながら私は言いたい:音楽家はA,B,C (音階)など音符を想像することは可能だろう。 (可能であれ ば1、2、3、でも出来るだろう、もっと言えば0、1、2でも可能だろう) 仮に自分の居間の1平方メートルの価値を計算出来るのであれば、複素数も分かり得るだろう。 紹介 (イントロダクション) 全ての実数は直線上に描くことができ、ゼロを真ん中にして左は負数、右は正数と表される。 同じように複素数は平面上に表される。水平線上(X座標)は実数部の部分、Y座標は虚数部。 それが全て だ!しかしながらそこから派生する代数の示唆は常に数学者を何世代にも渡り忙しくさせてきた。 Carl Friedrich Gauss (1777-1855) 彼は素数代数の開発に多大な影響を与えた人である。 複素数は多分名 前の付け方に問題があったので理解し辛かったのではないかと述べた。 (虚数や実数など難しい名前ばかり）
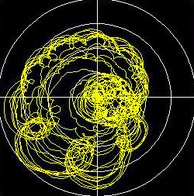
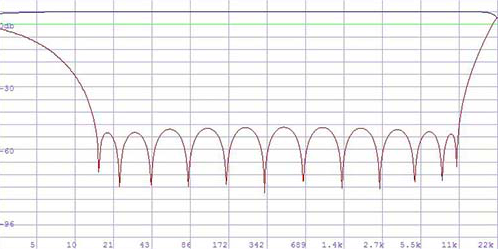
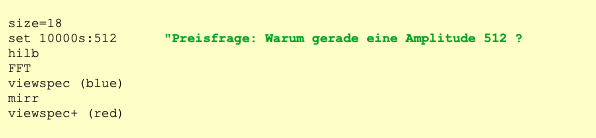
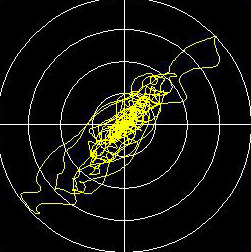
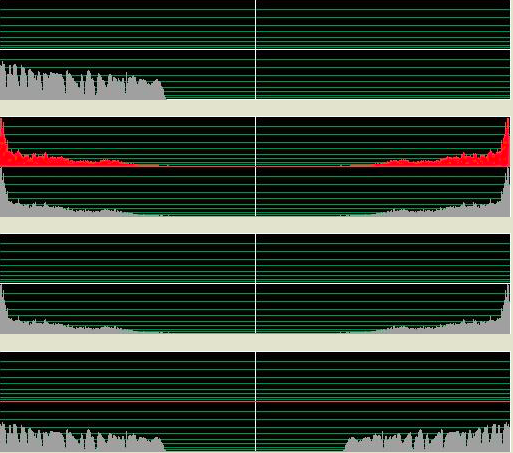
複素数を描写する為には2つの数値が必要。平面上にあるポイントの座標である。(XとY)その座標は直角を 成す。(デカルト座標もしくはXY座標)代替手段としては極座標、中心からの距離(半径)と角度。(位 相、フェーズ) 位相(フェーズ)は特に音楽のアプリケーションとして多大な意味を成している。 そして今やっとコンプレックスオーディオのところまで辿りついた! Complex audio 正弦音(サイン波)のオシレーションの波形は知っている通り必ずしも単純ではない。試しにサイン波を描 いてみると山の形状のように半分から下がったり上がったり円の半分ずつになっている訳では無い。何故こ の複雑なサイン波は耳にとって安易なオシレーションの形としてなっているのか、何故四角、三角、もしく は他シンプルなグラフィカルの形状ではないのだろうか。単純な理由がある。それは平面上に描写する際、 サイン波は平面の上にて最も基本的な動きに基づいているからである:円形上を一定速度にて動いている。 中心からの距離(半径)は常に一定である。(音量として認識する)回転のスピードも同じように常に一定 である。(周波数として認識する) もし回転が反対方向になったとしても音は同じように聞こえる!しかし一つの座標に投射すると変化は無い がもう一つの座標は逆になる。よって音自体は同じであってもポジティブやネガティブ周波数と表現する。 ポジティブとネガティブ周波数を一緒に重ねるとその現象を認識出来る。現象は音量の増幅、消去になる。 全てのモノシグナルは右周りと左周りの周波数の組み合わせとして解釈される。(音量はそれぞれ半々ず つ)一つの座標は完全であり、もう一つの座標はそれ自体が完全に消去される  例:)  時間領域上でのモノサウンド (Buffer size=18, 262144 samples, 約5.4秒間) 上記のフーリエ変換図  フーリエ変換の前はタイムドメイン内にて26万サンプルだったが、変換後はスペクトラム内は約26万周波 数になる。 図の半分より左は左周り、図の半分より右は右周り。 左端はゼロヘルツ、中心までは遮断周波数 (22050ヘルツ)これはポジティブ周波数。 中心から右に向かっては右端までミラーの形(右端はゼロヘル ツ)はネガティブ周波数。 キーショットカットのnを押すとバッファーのデータを数字として見ることが出来、 ポジティブとそのミラーされたネガティブ周波のアンプリチュードが同じであることが見て取れる。 (ただ右半分のイマジナリーパートは反転形:複素共役) バッファの右半分の全てのネガティブ周波数をゼロ(消去)にして、モノシグナルは実数部だけだが 右部分を消すと虚数部が再構築される。 VASPでは以下のように書き表す   右半分のバッファは消去  逆フーリエ変換 実数部(リアルパート)は(グレー)、新しい虚数部(赤)は全ての周波を含むが周波のフェーズは90度角度がシフトされた。よって全ての周波のサインにコサインが付属された形。 XY標識には下記のようなコンプレックスな動きが見られる。100ミリセカンドの部分。
 David Hilbert (foto Wiki Commons) Hilbert転換は元々実数部しかないオシレーションの虚数部を再構築可能にした。 (これまで説明したこととHilbert転換の違いは音量係数とゼロヘルツと遮断周波数が特別に扱われている こと)ステレオシグナルと同じように保存出来る。左は実数部、右は虚数部。私達の耳には両方の部分は同じように聞こえるが一緒になると時間の流れの中にて2次元の動きになる。そ れをコンプレックスオシレーションと呼ぶ。勿論、Vaspではワンステップにて可能:  これまで記述したことは一体何を目的としているのか? 多くのエフェクト、トランスフォーメーションもしくはモジュレーションは内在的にコンプレックスに作用しており、かつ実行可能である。 多くの機能はコンプレックスの方がリアルより機能する。 分析的なプロセス、例えばエンペロップ検出、(デテクション)ピークデテクション等はコンプレックス上の 方がより信頼性があり確実になる。特に全てのスペクトラル現象はコンプレックスのみ理解され得る。 そして完全に周波数と時間の繋がりを理解したい場合、コンプレックスの環境下でないと不可能である。 DSPプログラマーにとっては必要不可欠な考え方であり、ソフトウエアを通じて創られる音を予め予知した り、創造しながら作り上げていくユーザーにとってはまさしく必須のプロセスになり、エクスペリメンタル な音を構築するためには本当の意味においてその価値を習得出来得る。VASPは殆どの作用はコンプレック ス上にて行われる。(オペレーションのいくつかはコンプレックスかリアルか選択可能)よって全ての重要 なバッファーは2チャンネルにて実行される。 ••• 上記のHilbert転換は周波ドメインを得るために全体論としてFFTを使用している。周波ドメインの中にてネ ガティブ周波数を消去。勿論これらのことはリアルタイムのコンテクストの中では不可能。 その代わり、アルパスフィルターを使用。アルパスフィルターは名前通り、周波シフトを同時に行いながら 全ての周波を通していく。 1インプットと2アウトプット。セカンドアウトプットの全ての周波は最初のアウ トプットに対して完全に90度フェイズシフトされる。 [注意:]これはタイムシフトでもディレイでもな い!もしディレイ等を考えたければ全ての周波数には違うディレイがあると言える。 詳しく説明すると1つのアウトプットはマイナス45度になり、もう1つのアウトプットはプラス45度のフェイズシフトになる。合わせると90度になる。そのようなフィルターはVASPにもある:  上記のフィルターはBernie Hutchins氏の係数を使用した6-poleアルパス[この人には感謝しかない! フィ ルターの理論は机上の論理故、IIRフォルターの効率的な良いデザイン(構成)は専門知識だけでなく経験や 直感力が必要である。Hutchins氏は電子工学が専門。 1975年に係数を考案し世間に公表する前に60年 代、Harald Bode氏とBob Moog氏が単純なアルパスフィルターを使用した周波シフターを世に広めた。 (私は70年代にBode氏の周波シフターを使用していた。そのシフターに内蔵されたアナログアルパスフィ ルターはHutchins氏の技術には全く及ばなかった。Georg Danczul氏はEOAの仲間達には既に名を知られ ている人だがこのGeorg氏は70年代にさらに精密な周波シフターを私のために再構築してくれた) アナログエレクトロニクスに興味のある人はぜひBernie Hutchins氏のELECTRONOTESを見逃さないで欲 しい http://electronotes.netfirms.com] IIRフィルターはアナログでもデジタルでも関係なくフェーズはリニアではないが少しの遅れが生ずる。(こ の場合2~3サンプル)この意味するところは、オリジナルのシグナルは残らず、非常に似ている異なるシグ ナルに置き換えられるー他に避ける方法はない。しかしVASPでは違う。 VASP: フィルターは双方向的。オリジナルは左チャンネルのまま(実数部)、右チャンネルは90度フェイ スシフトされる。他のフィルターと同じように双方向的か一方方向か選択出来る。やり方としてはマイナス もしくは=を文頭に書く。(以下は書き方の表示) =hilb 双方向的(ディフォルト) -hilb 一方方向  フィルターのスペクトラム(以下参照) ポジティブ周波数は青色、ネガティブ周波数は赤色 周波数特性は図より分かるようにポジティブ周波の周波数特性は直線になり、ネガティブ周波は15Hz以下 と15khz以上の部分は残り、それ以外の部分は省かれている。(6db上がっていることは正しいので気にし ないで) これをVASPスクリプトに書くと  (緑の行は何故アンプリチュードは丁度512なのか誰か分かる?と表記されている中訳部になる) もしHILBのスペクトラルオペレーションのようにフィルターが完全であれば赤いラインはここにはないし、 全てのネガティブ周波はアンプリチュードがゼロになるだろう。低い周波数のシグナルに精密さが必要な場 合、HILBを推奨する。 ステレオをコンプレックスとして見た場合 放送工学ではステレオにて放送を始めてからPhase correlationメーターを使用している。それはオシロス コープのことであり、フェイズの状態がステレオシグナルの中にてどのような位置にあるのか見てとれる。 経験則:左下から右斜め上に基本対角線上にならなければならない。もしその対角線上であればモノの機械 でも音材を失うことなく聞くことが出来る。もし反対(右斜め下から左斜め上の線状)ならば消去(音のデ リート)が起こる。VASPではXYグラフィックスとしてゆっくりと表示される故にコンプレックス波の動き を理解し易くなる。(キーボードのショートカットキーのbを押すと早いバージョン、xならゆっくりなバー ジョンとして表示可能)  上記の図より 左図:左のチャンネルのみのシグナルはXYグラフィックス上ではX座標のみの(横)動き 右図:右のチャンネルのみのシグナルはXYグラフィックス上ではY座標のみの(縦)動き  上記の図より ステレオの真ん中のシグナルは左図の動きになる 左右のフェイズが交換された場合、右図のような対角線上になる。 原則として問題ないが両チャンネルを合 わせるとデリート(消去)される。ケーブルが故障していたりすると右図のように間違いにもなるがそれを 要求し敢えて使用することもあり得る。(stereo enhancer) 通常の2つのマイクより録音されたシグナルではXYグラフィックスは以下の図のようになる  コンプレックスとして見ると上記の図は周波の違うポジティブ回転の動きとネガティブ回転の動きを合わせ たもの(何がポジティブか、ネガティブかは定義による。通常反時計回りの回転をポジティブと呼ぶ。) VASPではそのミックスをそれぞれ分けられる: alf(alias filter)は修正されたHibertアルパスフィルターであり、ポジティブ周波を通してネガティブ周波を 抑え込んでいる; alf- はその逆(ポジティブを押さえ込みネガティブ周波を通す) その両方を組み合わせれ ばオリジナルのシグナルに戻る。  linksdrehend左スピン、 rechtsdrehend右スピン、complex=stereo コンプレックスはステレオと同じ エイリアスフィルターと名付けた理由はコンプレックスドメインの中の第1のエイリアス周波に反対方向に 回ることで認識されるから。(第2のエイリアス周波は同じ方向に回転する等々)このコマンドはもう一つ のモードがある:alf.split これはポジテイブ周波の実数部は左チャンネルに置いてネガティブ周波の実数部 は右チャンネルに置く。 結果は修正されたステレオパノラマ。もしリピートする場合は常に新しいステレオ 環境を生み出すことが出来る。 そのスクリプトは以下のようになる  (ヘッドフォンを使用して聞くべき) 音源は吹奏楽の行進の録音。窓辺にて2つのマイクを使用し録音したもの。 splitする度にパノラマが変化し、動きの方向が僅かに変化し、家の壁からの反射音の位置も変化していく。 complex audio in VASP これまで述べてきたようにほぼ全てのプレセスはコンプレックス上にて作用する。しかし意識下にて機能す る。詳しく言えば真にリアルな音を使用していく場合(モノ、コンプレックスに準備していない音素材)期 待している結果にならない場合があるということだ。 例えば周波数のシフト:  オペレーションはコンプレックス。しかし結果はただのリングモジュレーションかつ2サイドバンド、典型 的な荒さを引き起こす。(また不必要に他のチャンネルにフェイズシフトがある) 真のリニア周波シフトになるにはまずモノシグナルをコンプレックスシグナルに準備し直す必要がある。  コンプレックスオーディオを意識的に操作することはVASPの基本である! 殆ど全てのプロセスはコンプレックス故、これはコンプレックスだ、コンプレックスでないという列記はな い。1つの方向に回る周波数のシグナルは分析的シグナルと呼ぶ。(アナリティカルシグナル)なぜならサ ウンド分析の複数の基本だからだ。 Complexes Spectrum サウンドのスペクトラムはモノ(リアル)、スペクトラムは常にコンプレックス。 下記のように試せる:  結果は? ステップ バイ ステップ : 音がその音の時間がリバースされた音とミックスされた!(音自体はモノでもステレオでも良い) フーリエ変換は基本的にはコンプレックスのみにて作用する!  [リアルなFFTは存在する。それをRFTやRFFTと呼ぶ。多くのプログラマー達はRFFTでリアルスペクトラ ムを得ることが出来ると間違えて考えている。有り得ないことだ! モノシグナルはスペクトラムのバッファーの半分から下の部分と半分から上の部分はシンメトリック故、半 分から上の部分のみ計算する必要がない] VASPにもRFFTがある。このようなケースの場合、2倍早く処理出来る。しかし上の半分のバッファーは空 になる。上の半分の再構築はsymm.cjgによって可能。 知ってるようにスペクトラムは独立した音として表れるし、実際に聞こえ、かつ使用可能。 そのような音はどのような状況でもコンプレックスになる。 スペクトラムの音は通常右回り、そして左回りの周波のミックスである。しかしながら多くのスペクトラム 内のオペレーションは右周りなら右周りだけ等、1つの回転下の方が使い易い。(しかし、間違えないで: スペクトラムの中にて周波として聞こえるのはタイムドメインの中ではその時間の瞬間:1つずつのサンプ ル ー そして反対のもの>>SPILLING THE BEANS #9 Dellenhammer & Beulenhammer) 分析的なスペクトラムを得る為にはタイムドメインの中にて上半分のバッファーは空のままに、もしくは clear.uにて消去。(スペクトラム内のHilbertトランスフォーメーションのトリビアルなメソッド) スペクトラム内の有名な例はコンボリューション(convolution)というコンプレックスオペレーション。 2つの音のスペクトラムがモジュレートされる、つまりサンプルずつに掛け算されるということ。勿論掛け 算はコンプレックスである。そうでない場合の結果は両方の時間の方向においてリバーブされる... 2つの音のコンボリューション出来るVASPスクリプト(バッファーに十分なスペースが無いといけない、 何故なら結果は2つの音の長さが足し算になるから)  vmulは1つのバッファの内容と他のバッファーのコンプレックス掛け算。勿論Macroとしても書ける: CONV。しかしMacroでない方はスペクトラム内の編集が可能。典型的なコンボリューションの鈍い音はコ ンプレーサーブースとして使用して訂正可能。(以下参照)  (1.5はコンプレッションの要因、10hzはスペクトラム周波数とは関係なくエンべロップディテクターの フィルターの設定) complex audio in AMP アナログエフェクトを使用する際には(例えばBode周波シフター)内部的にコンプレックスにて動くかど うかは関係なく同じようにAMPのコアモジュール(オブジェクト)を使用する時でも心配する必要ない。 コンプレックス上にて動く全てのモジュールはアルパスフィルターにて構築されたものがスタンダード。 モノインプットを受けてモノアウトプットを出す。(もし特別なことを要求しなければ)  基本的にはAMPでは特にコンプレックスかどうか注意する必要はないしコンプレックスパラメーターも無 い。(やり方を知っていればパラメーターはコンプレックスに接続も可能) もし内部的にコンプレクスで動く複数のモジュールに接続する場合やコンプレックスドメインを出て全ての モジュールでアルパスフィルターを使う場合、ぎこちない状況になる。その場合ではコンプレックスアウト プットとしてそのモジュールのアウトプットをコンプレックスアウトプットにする方が良い。 フェーズスピンとエイリアスフィルターを周波シフトに後付けたものについてのスクリプト 以下添付図の詳細: Liefert complexen output durch c:カッコ内にcが記載されているのでアウトプットはコンプレックス übernimmt complexen output durch ** :**が記載されているのでインプットはコンプレックスになる liefert aber wieder einen mono output :カッコ内にmが記載されているのでアウトプットはモノになる  *** コンプレックスオーディオの冒険に何も立ちはだかるものはない！ akueto G.R. (c) Günther Rabl 2011- 13 Comments are closed.
|
Günther rabl
|
CHIEKO MORI © 2023